Evaluating Portfolio Performance
Imagine a highway consisting of three lanes – the slow lane, middle lane and the fast lane.
Which lane would you take to get to your destination?
All lanes have the potential to get you to your destination, but each lane has a different speed and the associated risk of “accidents”

Goal is to maximize Return over Risk
Getting to your destination faster without taking too much risk is the goal when driving, right??
Similarly for a portfolio, getting the highest return possible without taking too much of risk is the goal of a portfolio manager
In order to evaluate a Portfolio, one of the important metrics therefore is the ratio of return over risk
Sharpe Ratio
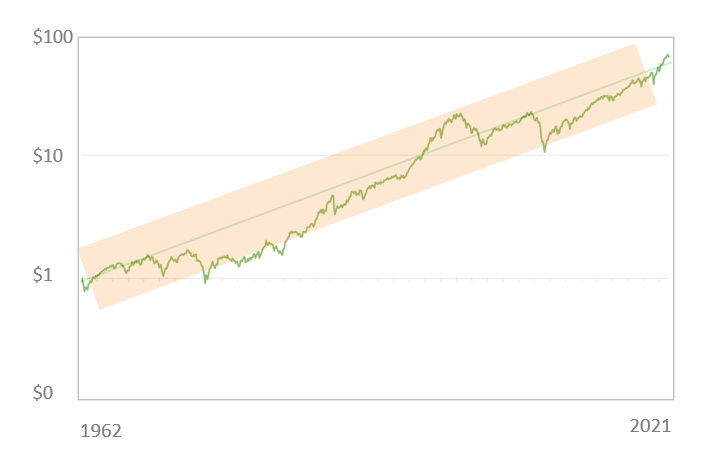
Consider the stock market. The annualized return is the numerator. In this case it is ~9%
Risk can be measured in two ways. One measure is the standard deviation, which is the extent to which the portfolio growth deviates from a straight line; in other words, if you want the portfolio to grow consistently over time, the standard deviation needs to be low.
The ratio of the annualized return over the standard deviation is called the Sharpe Ratio
Definitions: Standard Deviation, Sharpe Ratio
MAR Ratio
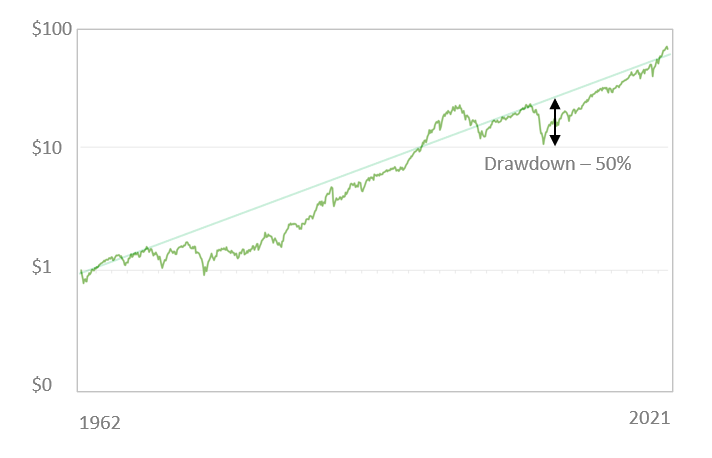
A second way of measuring risk is the maximum drop that the portfolio has seen over time. For the stock market, this was during the 2008-2009 time-frame, when it dropped by almost 50%. This is called the maximum drawdown.
The ratio of the annualized return over the maximum drawdown is called the MAR Ratio
Definitions: MAR Ratio
Drawdown Recovery Time
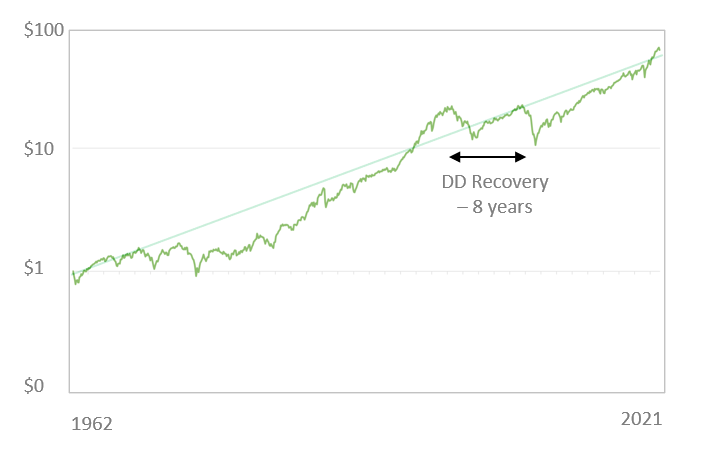
Another important metric is the maximum drawdown recovery time, which is the amount of time that the algorithm takes to recover from a drawdown
For the stock-market, the maximum drawdown recovery time was from September 2000 to October 2008 – 8 years
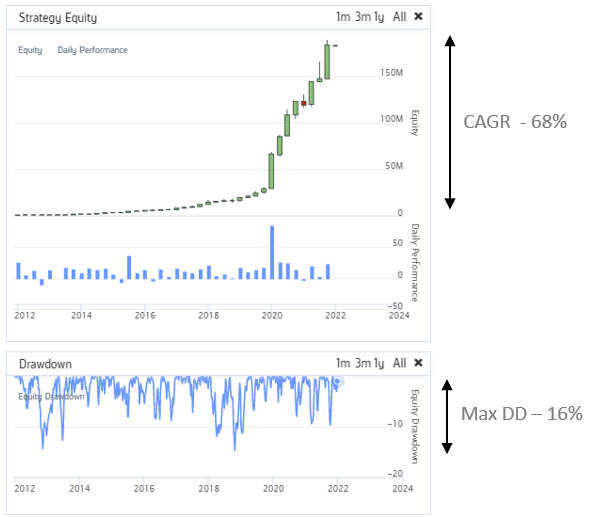
Putting it all Together - I
Consider one of our algorithms that we use in our portfolios.
The algorithm keeps switching between stocks, bonds, gold and volatility assets in an attempt to maximize the ratio of return over risk.
The MAR ratio of this algorithm is 68% divided by 16% = ~4.2

Putting it all Together - II
The standard deviation of the portfolio over time was around 25%
The Sharpe ratio of this algorithm is therefore 68% divided by 25% = 2.7
The maximum drawdown recovery was from September 2012 to March 2013 = ~7 months

Putting it all Together - III
Going back to our lane analogy, what if you could diversify not just between the lanes that get you to your destination, but also the vehicles you use to drive on those lanes. Mini Van (Slow-moving but dependable), Sports Car (Faster, changes lanes more often), Bike (Fastest, weaves through traffic, but higher risk of accidents)
We use the term Time Diversification to describe our unique approach where we also diversify between different strategies including long term, swing trading and day trading models.
This helps us strive to avoid large drops in the market and potentially even make higher returns when the market drops. This also helps us recover from drawdowns much faster than traditional approaches



